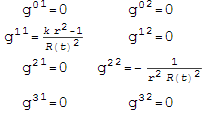
这是去年为了算宇宙学作业而写的一个小程序库。

使用了网友提供的某神奇语法（过了半年引源竟然死活找不到了，罪过罪过….）,实现了类似面向对象的简单语法。程序本身还缺乏面向对象的其他一般特征，但对于完成一般的张量计算，可视化输出张量的操作等，还是够用了。

程序中所有内容的数学定于源自梁灿斌教授的《微分几何入门与广义相对论》，张量指标分上下，一些张量的缩并方式（如里奇张量）可见注释。

程序的主要功能有

Demo

Mathematica  

# 创建两个上指标（上指标用u表示，下指标用d表示），维度大小为{4,4}的张量
T=new[Tensor["uu",{4,4}]]
# 用一个List来初始化张量
T.setTable[someList]
# 改变张量符号
T.setSym['\[rho]']
# 查看张量值（返回一个List）
T.showTable[]
# 可视化查看张量值(返回一个List，每个元的内容是张量符号=张量值)
T.showEqu[]
# 显示张量的所有信息
T.info[]
# 张量的转置
tensorTranspose[TUDU, {1, 3, 2}]
# 加法（维度不对会有提示）
T1~tPlus~T2
# 减法 （维度不对会有提示）
T1~tMinus~T2
# 乘法
T1~tensorProduct~T2
# 缩并 （维度大小不对会有提示）
C[gUU, dgDDD, {2,1}]
# 坐标导数
tensorCoordinateD[T, v]
# 张量导数（需要提供联络张量）
tensorD[RUDDD, v, GamaUDD];
# 返回关于第3,4,5个指标对称的对称张量
tensorSymPart[T,{3,4,5}]
# 返回关于第3,4,5个指标反对称的反对称张量
tensorAnSymPart[T, {3, 4, 5}]

下面是简单的demo和一些宇宙学相关的计算，看完了就会用了