\(e^t\)与旋转矩阵的操作性理解
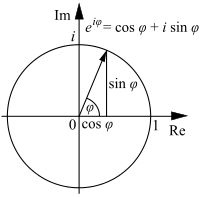
是神马含义?呢??
旋转矩阵是神马?怎么着他就能代表一个旋转了??
这些问题有一个共同的特点:大部分相关的主流中文教科书从没有把这些东西讲解到直观的令人信服,虽然说数学是一门倡导抽象思维能力的学科,但是把数学知识可视化,直观化一方面方便记忆,另一方面使你真正可以理解这种数学过程,把他更为自然的的应用在你的日常学习中。
回到我们的问题,这次我们往前说。
我们在小学阶段学会了基本的加减乘除分式计算,进入初中,才第一次接触到乘方和根式,比如代表四个3相乘,而表示两个相乘可以得到2的数(约定俗成是个正数)。,老师会说这个数如果平方一下再开立方,就会得到4…….至于么,老师擦了擦汗说5.64534是个有理数,可以变成一个由整数组成的分式,你把它变成分式后按照刚才那种理解,就是一个满足先自乘XXX次后再开XXX次方后得到5的这样一个数。你说:“好吧,那么是个啥呢?总不是一个有理数吧。”
“你就先这么理解吧,你取\pi的有限位,可以得到按照上面那种理解方式的一个数,然后你取无限位,就得到这个数了。取无限位的过程你上了大学就知道了,反正就是一个奇奇怪怪的数,呵呵”
“………………….”
不管怎么绕过来绕过去,我们小时候几乎是根深蒂固的把这样一个指数形式理解为满足上面那种性质的一个数,即“把a连乘b次,如果b不是整数,好像还得开个方神马的,反正就是这样乘来乘去开来开去的去操作a”,所以当我们第一次见到这样的形式,一定会被吓坏了:这个东西我还没有搞清楚呢,你就给我来个,这个游戏How to play? 你让我怎么去操作那个?自己乘以自己次??
好吧,让我们(暂时)忘掉你的中学老师,问问牛顿怎么看吧
“啊,伟大的牛顿,是个啥啊?”
“用我发明的微积分,把它展开,它就是”
“额,你这是个啥?”
“用我发明的微积分,他就是 …..”
“能说的更明白一些么?”
“用我发明的微积分…..”
把展开后,我们得到了新的理解:“这个东西不用再绞尽脑汁怎么去自乘N次开N次方这样去操作e了,我们只需要按照展开式那样,去操作t就行了,然后把这….好吧,无穷多项…..操作加在一起就行了”
这样做的好处是方便可视化,下面有请栗子君
的可视化
此处取
还要记得我们的展开式
我们这样去理解这个式子:“我首先定义一个线性的变换t,如果一个数乘以t,那么这个数变为原来的t倍,现在再定义一个对变换进行变换的函数,它把t这个线性变为如展开式所示的变换,如果一个数乘以,相当与对这个数进行这个操作
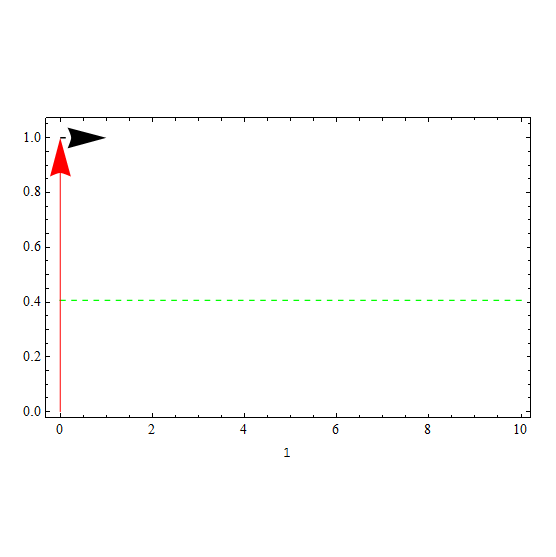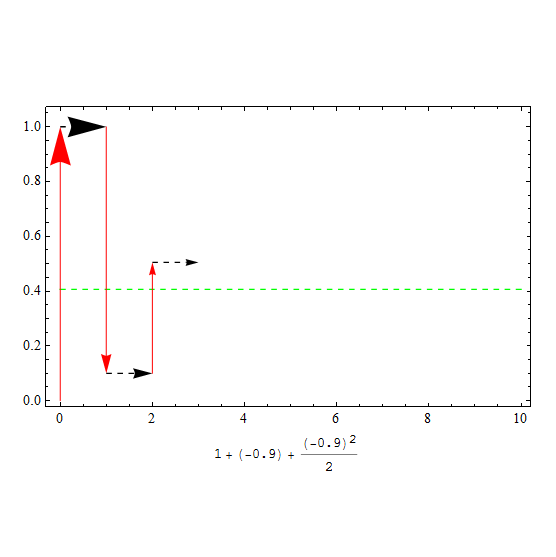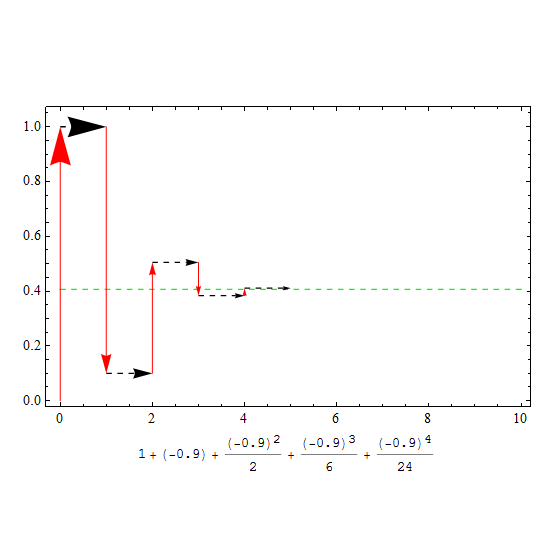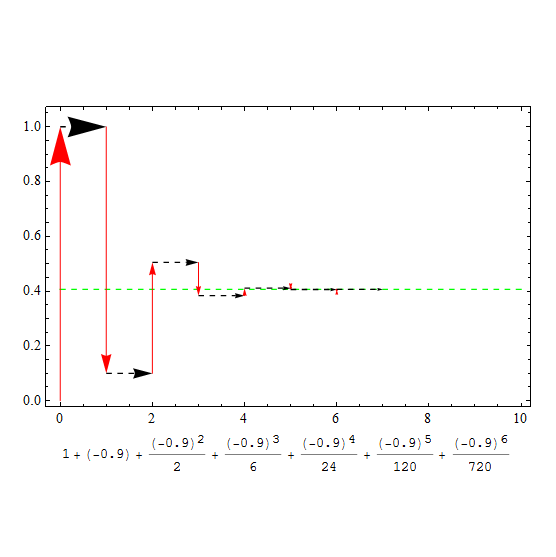
图:图中红色箭头表示每一项的操作,绿色虚线代表\(\text{e}^{t}\)的数值结果
看起来似乎是很平凡的结果
的可视化
同样的,首先定义一个线性变换,一个数乘以,则其值变为原来的倍。
复数域中,变为倍,意味着其模长变为t倍,辐角增加

图:复平面图,\(A_0\)为原始复数,途中红色箭头为每次的操作,绿色虚线为\(\text{e}^{\text{i}t}\)的数值,红绿线之间的夹角就是t(rad)
这个结果看起来就可爱一些了
旋转矩阵的可视化
我们有一个初始的向量,记为
定义一个线性变换
的意义是把的长度变为原来的倍,并逆时针旋转(这和上一个例子一模一样啊!)
使用作为变换操作的这一种理解
可视化为下图

图:图中红色箭头为每次变换的结果,绿色箭头为\(\text{e}^B\)的结果,红绿线之间的夹角就是\(\omega(rad)\)
的意义好直观啊,但是他和我们的旋转矩阵有什么关系呢?
可以(不那么可视化的)证明(留做习题),
这正是旋转矩阵。
同理,可以在e的指数上面放上各种乱七八糟的线性操作,按照级数展开这样理解,可以得到一个新的变换,这些变换往往具有某些物理意义。这就是的操作性理解方法。
扩展阅读:
《Visual Complex Analysis》 by Tristan Needham
《Linear Algebra Done Right》by Sheldon Axler
《Linear Algebra and Its Applications(Third Edition)》 by David C. Lay



